|
656010, Алтайский край, город Барнаул,
ул.Эмилии Алексеевой, 53 корпус 1,39 корпус2
Телефон / Факс: +7 (3852) 22-62-77
[email protected]
|
Геометрические фигуры и ихКартинки названия геометрических фигур (30 фото)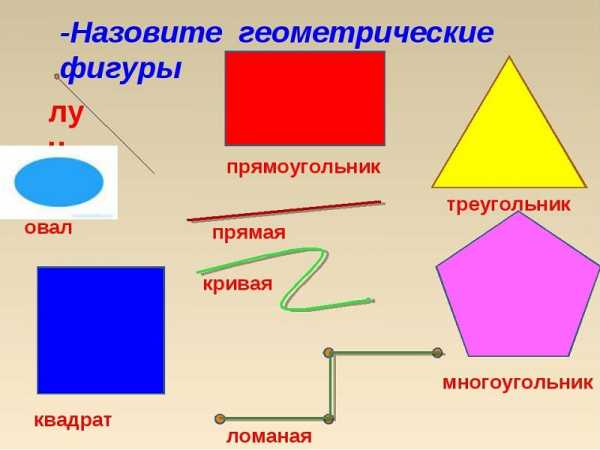 Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур. Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур. 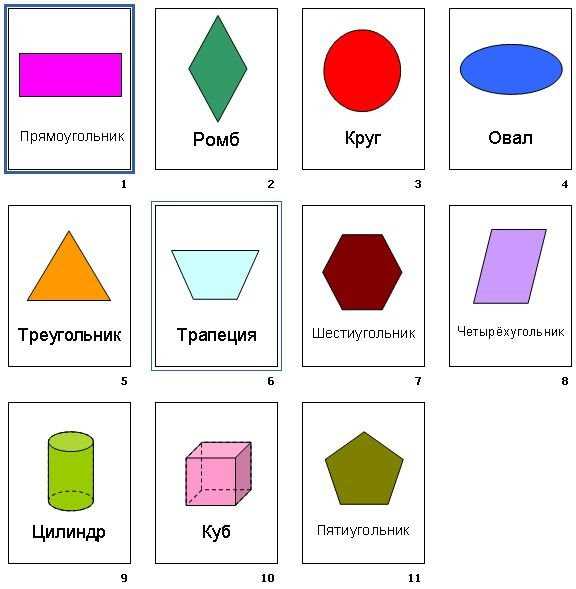 Прямоугольник, ромб, круг. Прямоугольник, ромб, круг. 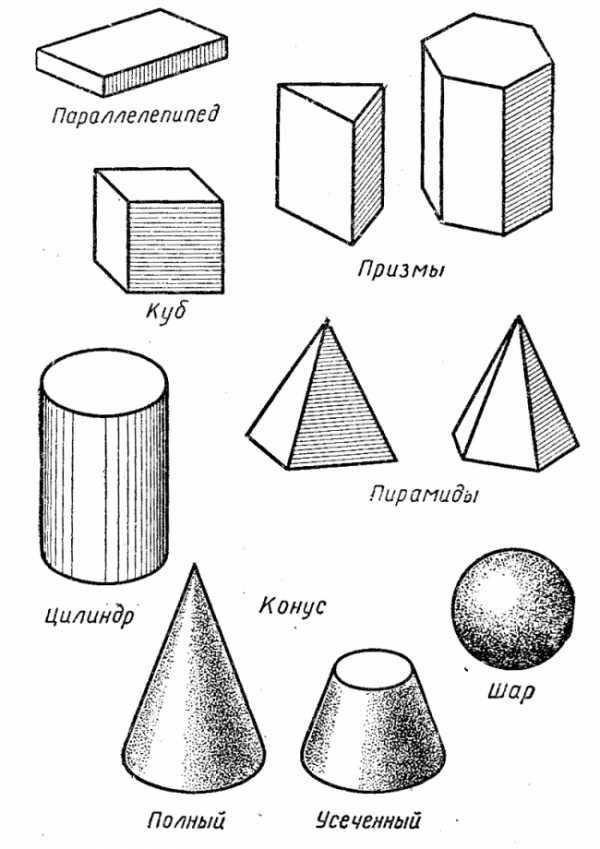 Параллелепипед, шар, конус. Параллелепипед, шар, конус. 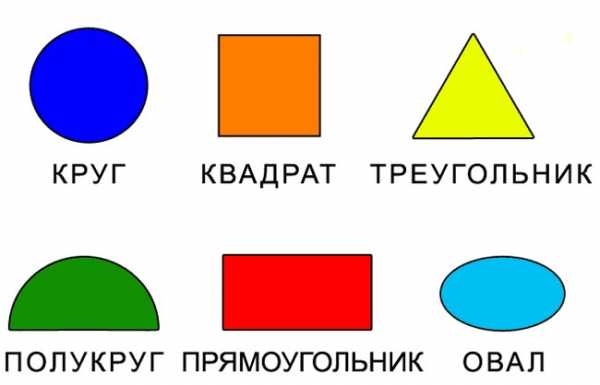 Круг, квадрат, овал. Круг, квадрат, овал.
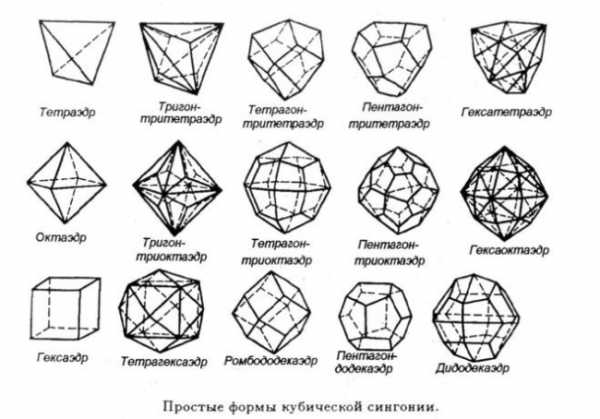 Сложные геометрические фигуры с названием. Сложные геометрические фигуры с названием. 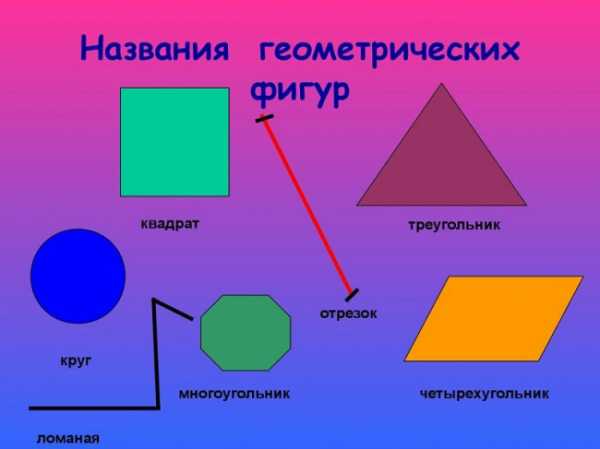 Ломанная, многоугольник, отрезок. Ломанная, многоугольник, отрезок. 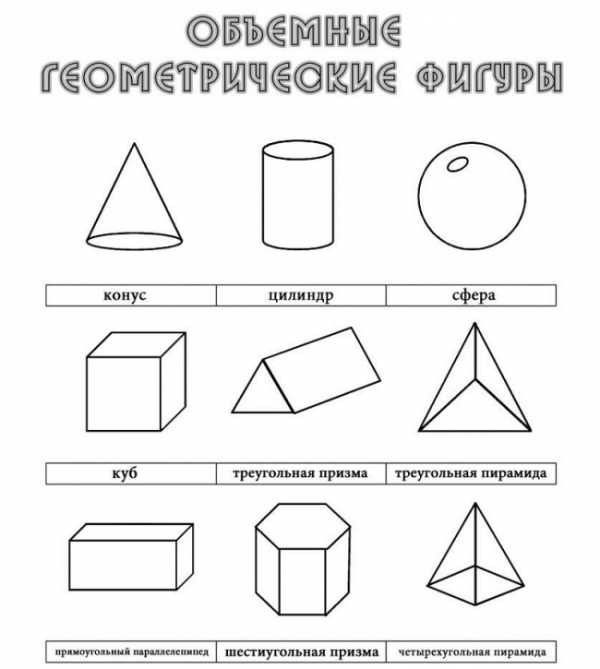 Конус, цилиндр, сфера. Конус, цилиндр, сфера. 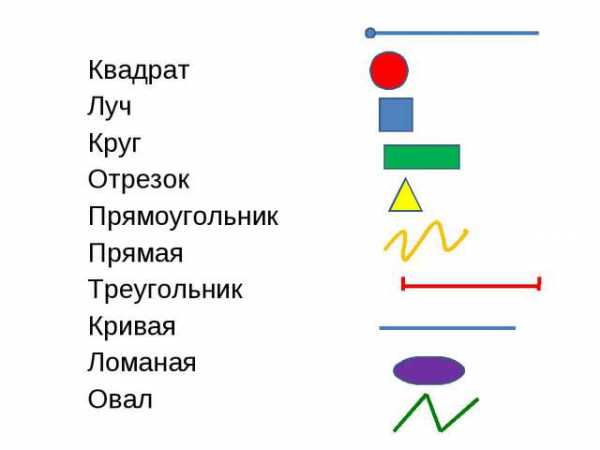 Картинка про название геометрических фигур. Картинка про название геометрических фигур. 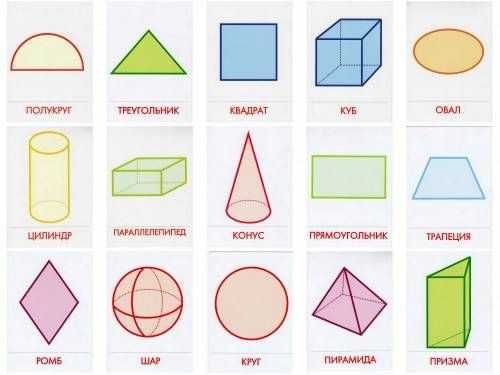 Полукруг, треугольник, трапеция. Полукруг, треугольник, трапеция. 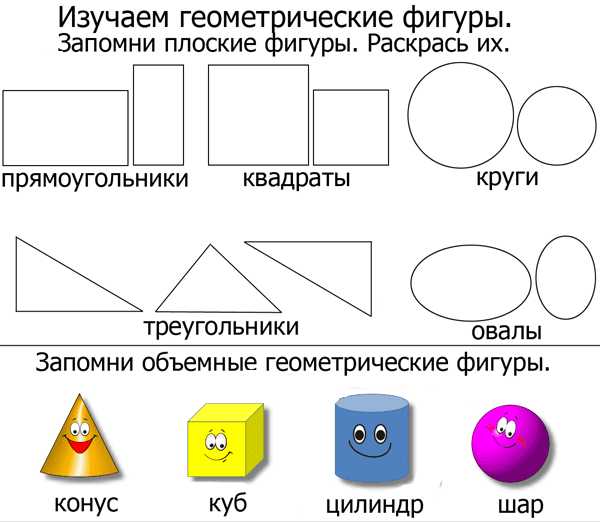 Квадраты, круги, овалы. Квадраты, круги, овалы. 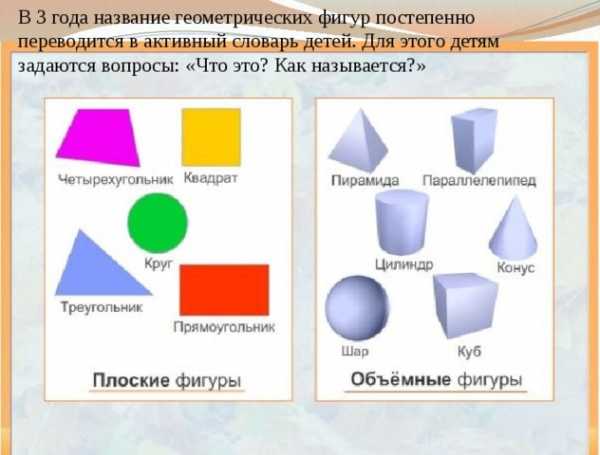 Разные фигуры из геометрии. Разные фигуры из геометрии.  Параллелограмм, восьмиугольник. Параллелограмм, восьмиугольник. 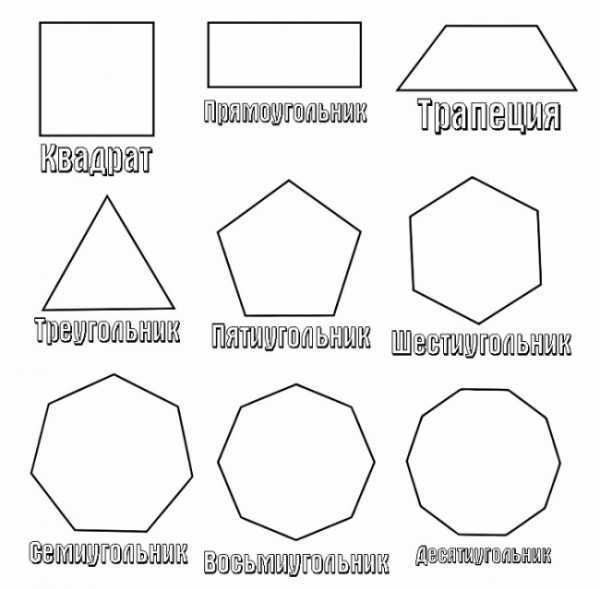 Квадрат, шестиугольник, семиугольник. Квадрат, шестиугольник, семиугольник.  Звезда, призма, сфера. Звезда, призма, сфера. 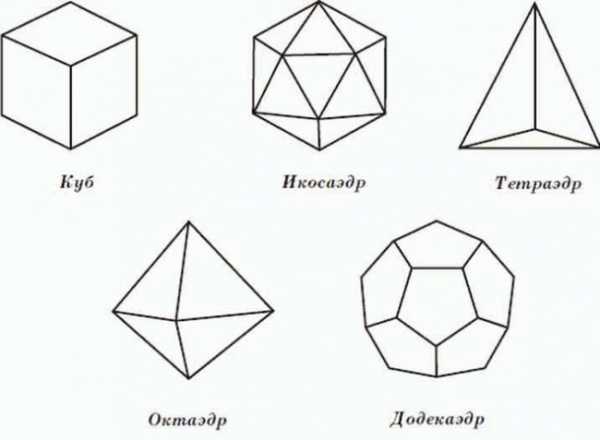 Предметная картинка про геометрические фигуры. Предметная картинка про геометрические фигуры.  Большой красный конус. Большой красный конус.  Оранжевый ромб. Оранжевый ромб.  Синий куб. Синий куб.  Название геометрических фигур Название геометрических фигур 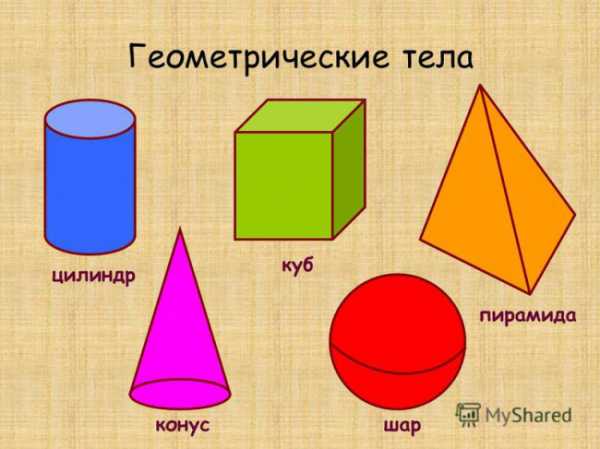 Геометрические тела. Геометрические тела.  Разные пирамиды. Разные пирамиды. 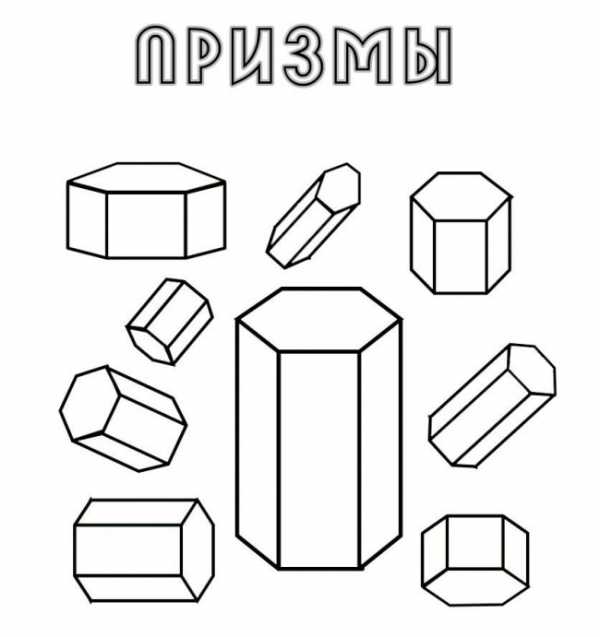 Простая картинка названия геометрических фигур. Простая картинка названия геометрических фигур.  Фиолетовый ромб. Фиолетовый ромб.  Красивый конус. Красивый конус. 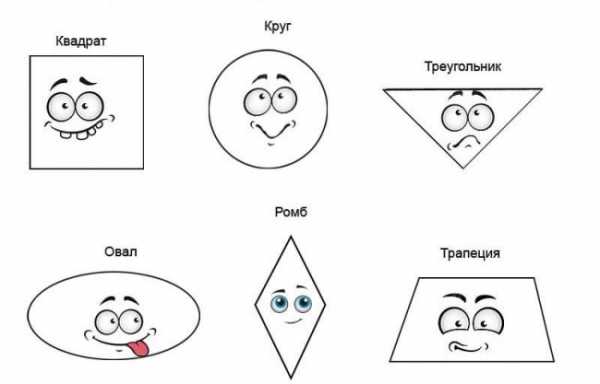 Овал, трапеция, ромб. Овал, трапеция, ромб. 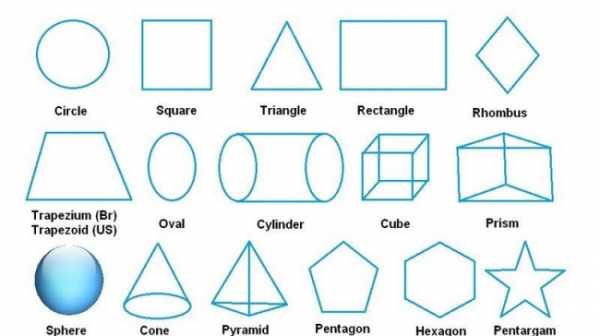 Много фигур из учебника геометрии. Много фигур из учебника геометрии. 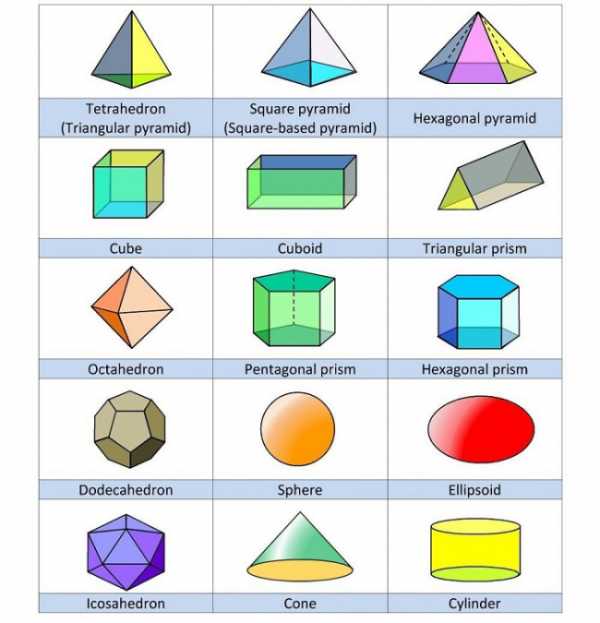 Куб, сфера. Куб, сфера.  Сердце, звезда, овал. 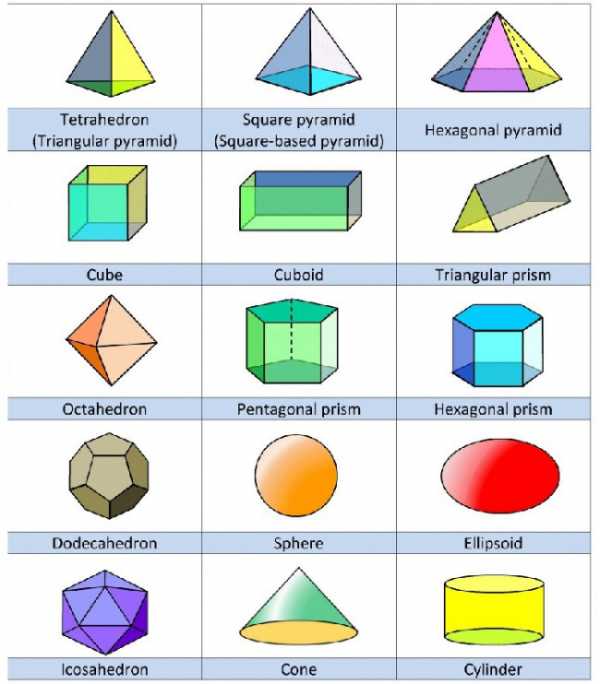 Геометрические фигуры и их названия. Геометрические фигуры и их названия. 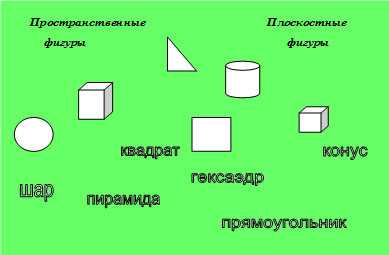 klike.net Геометрические фигуры и их названияЗдесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое - все, что подскажет вам фантазия. Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета. Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия. Также вам может понравиться наш онлайн тренажер по математике для 1 класса "Геометрические фигуры":
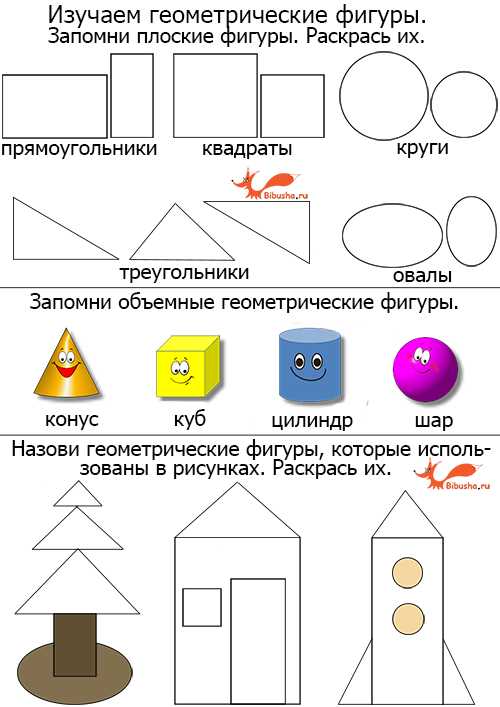
Онлайн-тренажер по математике "Геометрические фигуры 1 класс" поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник. Геометрические фигуры и их названия - Проводим занятие с ребенком:Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.
Скачать геометрические фигуры и их названия - Бланк задания - вы можете во вложениях внизу страницы.
Названия геометрических фигур - Карточки для распечаткиИзучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши. Скачайте вложения, распечатайте на цветном принтере бланк с карточками, вырежьте каждую карточку по контуру – и приступайте к обучению. Карточки можно заламинировать, либо наклеить на более плотную бумагу, чтобы сохранить внешний вид картинок, ведь использоваться они будут неоднократно. Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название. После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу. Скачать названия геометрических фигур - Карточки для распечатки - вы можете во вложениях внизу страницы
Карточки для распечатки с изображением плоских геометрических фигурС помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название. Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша. Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях
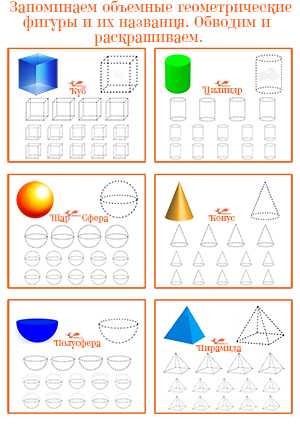
Объемные геометрические фигуры и их названия - скачать карточкиВ процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму. Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир. Скачать - Объемные геометрические фигуры и их названия - вы можете во вложениях внизу страницы
Также вам будут полезны и другие материалы по изучению геометрических фигур: Рисунки из геометрических фигур - Задания в картинках и раскраски Веселые и красочные задания для детей "Рисунки из геометрических фигур" являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: Геометрические фигуры - Раскраска для дошкольников Задания ознакомят ребенка с основными фигурами геометрии - кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры - Обведи и дорисуй Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги. Найди формы геометрических фигур в картинках Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга - Задание для детей Наложение фигур друг на друга - это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры. Свойства геометрических фигур для дошкольников Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур - Картинки с заданиями Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел - Задание для детей В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии Геометрические фигуры из бумаги - Вырезаем и занимаемся Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания. Счет до 5 - Картинки с заданиями для малышей Здесь мы выложили для вас счет до 5 - картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши: Игра "Что лишнее? - Геометрические формы" В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
bibusha.ru Геометрические фигуры ◼️ виды с названиями, определение и обозначение, основные свойства, интересные факты о простых и сложных фигурах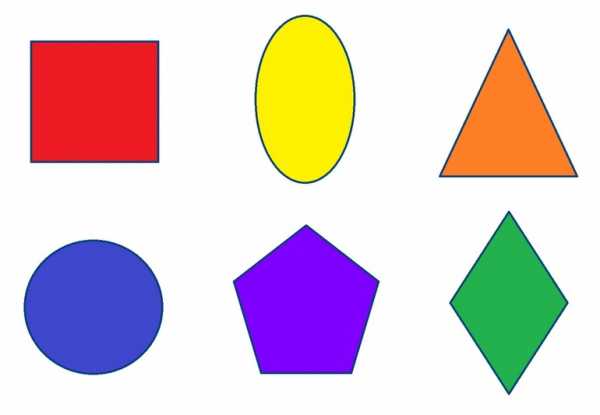 Общая характеристикаПредметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение. Основные понятия о составляющихКогда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.  Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия. Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc). Виды линий:
Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке. 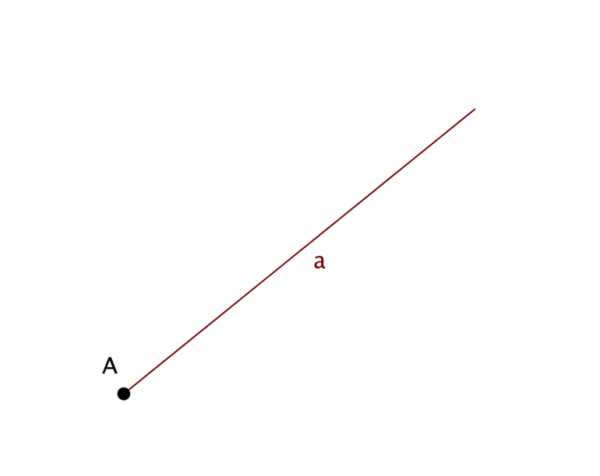 Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону. Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.
Стандартные объектыК основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом. Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У. Виды треугольника в зависимости от угла (У):

Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину. Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб. Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой. Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию. Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.
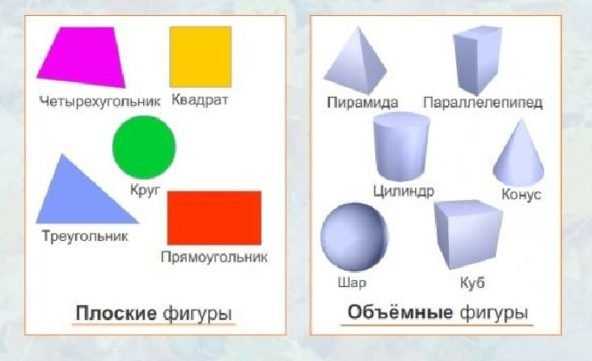
Сложные моделиВ сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция. Определение тела и пространства Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения. Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар). Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом. В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).  Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция. Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия. Объемные фигуры:
Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников. Виды многогранников: 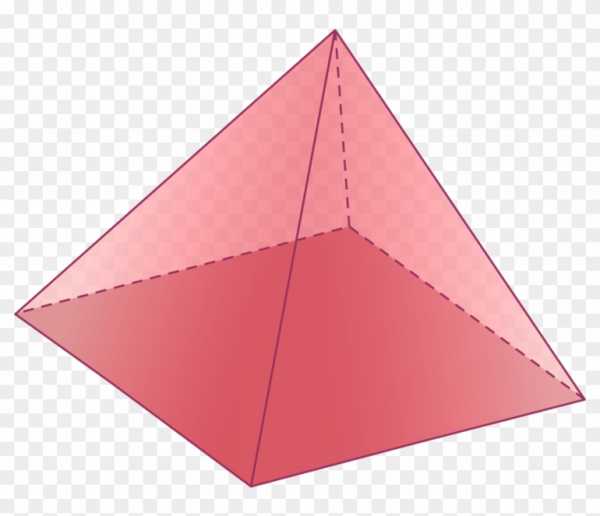
Познавательные игрушки детямГеометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении. Основной материал для обучения детей:
Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.  Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов. Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность. Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой. Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки. Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.
nauka.club Названия геометрических фигур в картинках (23 ФОТО) ⭐ ЗабавникГеометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.
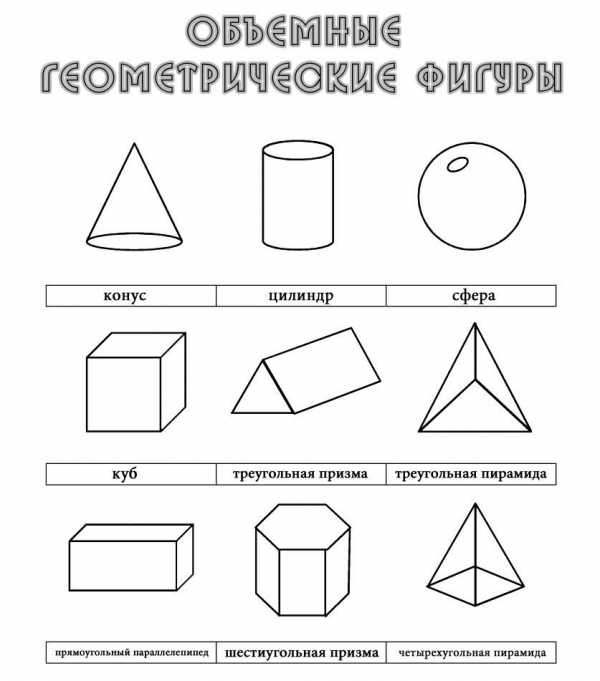 Объёмные геометрические фигуры
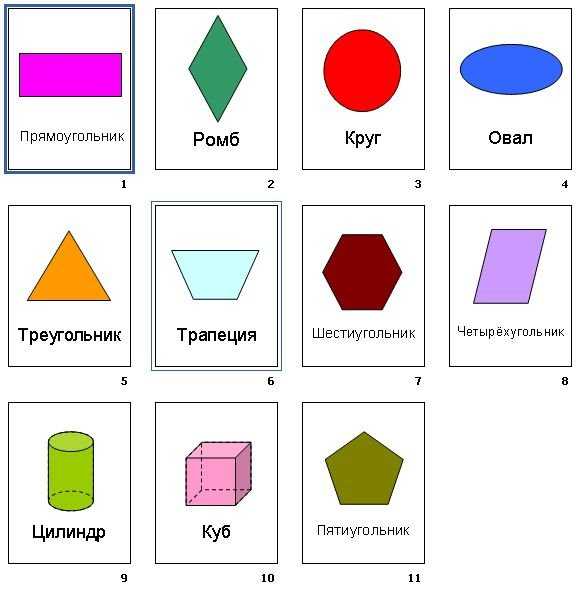 Разноцветные фигуры
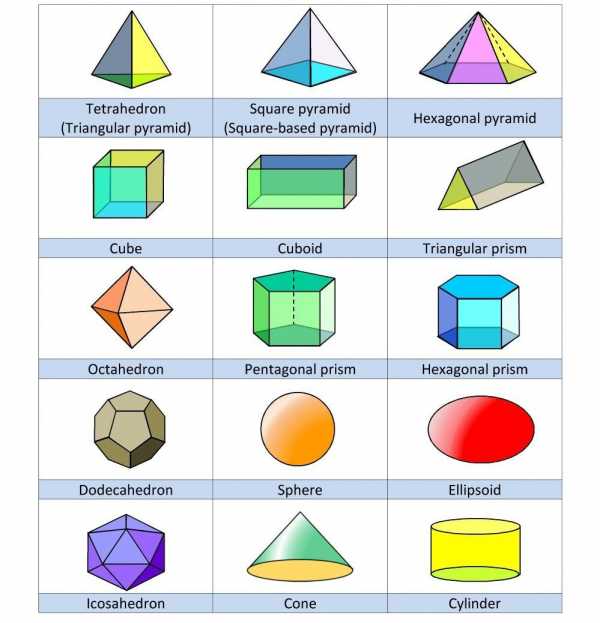 Названия объёмных фигур на английском
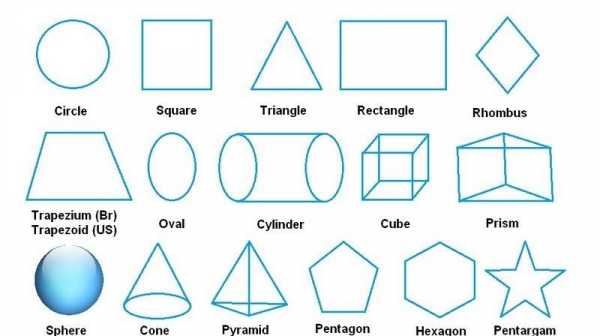 Синие фигуры с английскими названиями
 Синие фигуры с русскими названиями
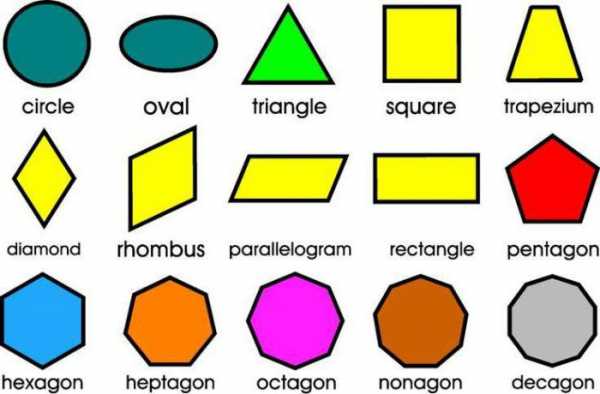 Разноцветные фигуры с английскими названиями
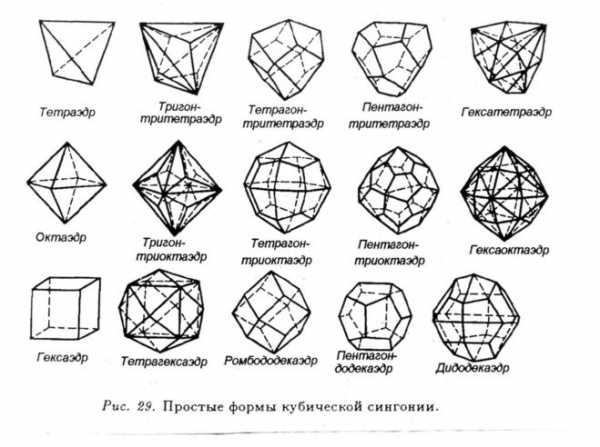 Простые фигуры кубической сингонии
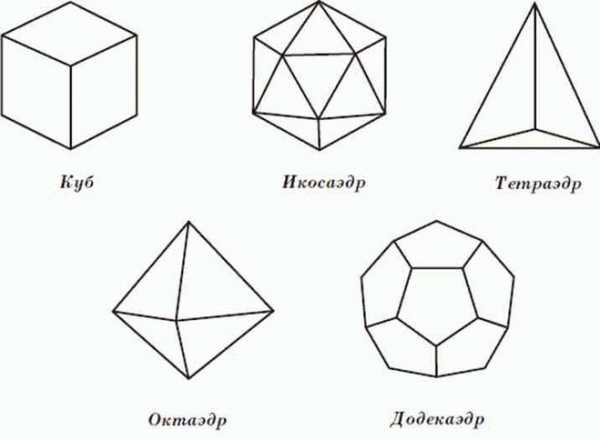 Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр
 Весёлые геометрические фигуры
 Shapes
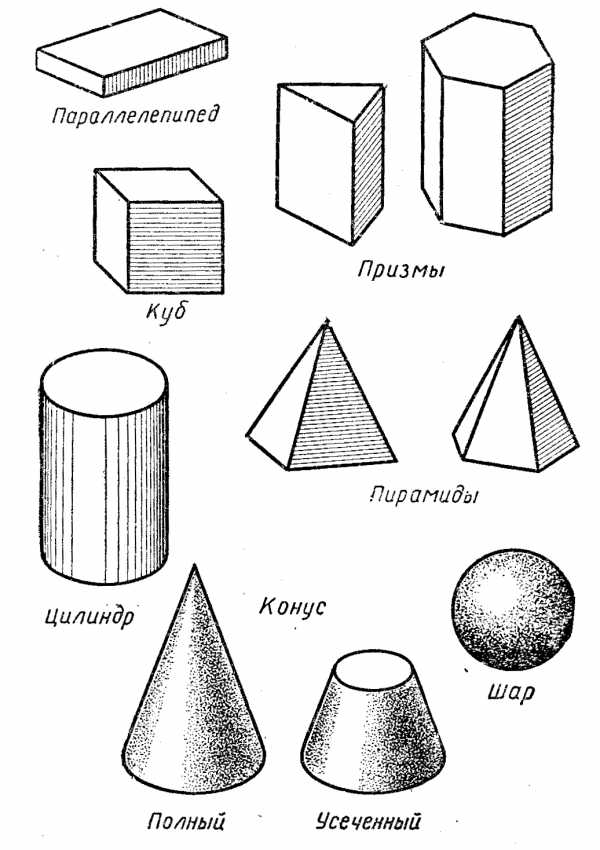
 Конус
 Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник
 Ромб
 Призмы
 Пирамиды
Ваша оценка очень важна: Загрузка... zabavnik.club Список геометрических фигур - полный перечень по алфавиту онлайн Список на этой странице для удобства поделен на буквы. Геометрические фигуры образуются множеством точек и ограничены числом линий. Перечень по алфавитуНашли ошибку? Выделите ошибку и нажмите Ctrl+Enter
kupidonia.ru 19Понятие геометрической фигуры. Виды геометрических фигур.Геометрическую фигуру определяют как любое множество точек. Если все точки геометрической фигуры принадлежат одной плоскости она называется плоской. Например, отрезок, прямоугольник – это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида. Так как понятие геометрической фигуры определено через понятие множество, то можно говорить о том, что одна фигура включена в другую (или содержится в другой), можно рассматривать объединение, пересечение и разность фигур. Точка – неопределяемое понятие. С точкой обычно знакомят, рисуя ее или прокалывая стержнем ручки в листочке бумаги. Считается, что точка не имеет ни длины, ни ширины, ни площади. Линия – неопределяемое понятие. С линией знакомят, моделируя ее из шнура или рисуя на доске, на листе бумаги. Основное свойство прямой линии: прямая линия бесконечна. Кривые линии могут быть замкнутыми и незамкнутыми. Луч – это часть прямой, ограниченная с одной стороны. Отрезок – часть прямой, заключенная между двумя точками – концами отрезка. Ломаная – линия из отрезков, соединенных последовательно под углом друг к другу. Звено ломаной – отрезок. Точки соединения звеньев называют вершинами ломаной. Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – его вершиной. Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и две точки на сторонах угла. Угол называется развернутым, если его стороны лежат на одной прямой. Угол, составляющий половину развернутого угла, называется прямым. Угол, меньший прямого, называется острым. Угол, больший прямого, но меньше развернутого, называется тупым. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми. Треугольник – одна из простейших геометрических фигур. Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков. В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии. Остроугольным называется треугольник, все углы которого острые. Прямоугольным – треугольник, который имеет прямой угол. Треугольник, который имеет тупой угол, называется тупоугольным. Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника. Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами. Диагональю называется отрезок, соединяющий противоположные вершины многоугольника. Прямоугольником называется четырехугольник, у которого все углы прямые. Квадратом называется прямоугольник, у которого все стороны равны. Многоугольником называется простая замкнутая ломаная, если ее соседние звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника, а ее звенья – его сторонами. Отрезки, соединяющие не соседние, называются диагоналями. Окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки, которая называется центром. Но поскольку в начальных классах не дается это классическое определение, знакомство с окружностью проводят методом показа, связывая его с непосредственной практической деятельностью по вычерчиванию окружности с помощью циркуля. Расстояние от точек до ее центра называется радиусом. Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром. Круг-часть плоскости, ограниченная окружностью. Параллелепипед – призма, у которой основание – параллелограмм. Куб – это прямоугольный параллелепипед, все ребра которого равны. Пирамида – многогранник, у которого одна грань (ее называют основанием) – какой-нибудь многоугольник, а остальные грани (их называют боковыми) – треугольники с общей вершиной. Цилиндр – геометрическое тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей, и перпендикулярных плоскостям оснований. Конус – тело, образованное всеми отрезками, соединяющими данную точку – его вершину – с точками некоторого круга – основание конуса. Шар – множество точек пространства, находящихся от данной точки на расстоянии не большем некоторого данного положительного расстояния. Данная точка – это центр шара, а данное расстояние – радиус. studfile.net Геометрические фигуры плоские и объёмныеЦели урока:
Планируемые результаты: личностные:
метапредметные:
предметные:
УУД общенаучные:
УУД личностные:
Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь. Тип урока: изучение нового материала. Методы: словесные, исследовательские, наглядные, практические. Формы работы: фронтальная, групповая, парная, индивидуальная. 1. Организация начала урока.
2. Актуализация знаний. Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь! Чтобы дойти до цели, надо прежде всего идти. Перед вами высказывание, прочитайте. Что означает это высказывание? (Чтобы чего-то добиться, нужно что-то делать) - И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели. - Начнем наш путь к достижению цели сегодняшнего урока. 3. Подготовительная работа. - Посмотрите на экран. Что вы видите? (Геометрические фигуры) Назовите эти фигуры. - Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы) - У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах. - По какому признаку вы разделили эти фигуры?
- С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые? - Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.) - Чему мы должны научиться на уроке? 4. «Открытие» нового знания в практической исследовательской работе. (Учитель показывает куб и квадрат.) - Чем они похожи? - Можно ли сказать, что это одно и тоже? - Чем же отличается куб от квадрата? - Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.) - Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную? ! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.) - Можно ли куб полностью (весь) прижать к парте? Проверим. - Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой? ! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.) ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.) ПЛОСКИЕ
ОБЪЁМНЫЕ
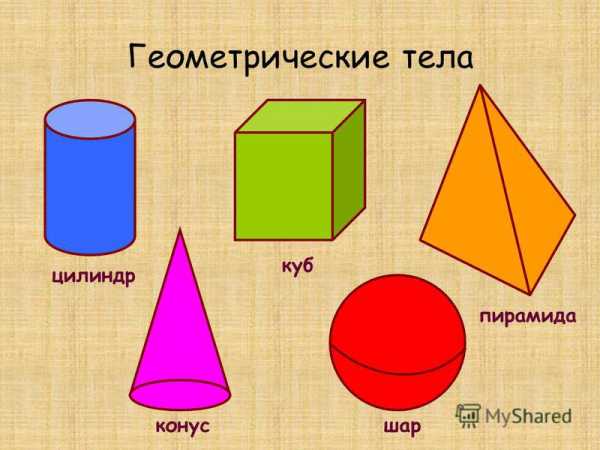
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед. 4. Открытие новых знаний. 1. Назовите фигуры, изображенные на рисунке. - Какую форму имеют основания этих фигур? - Какие еще формы можно увидеть на поверхности куба и призмы? 2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
- Предложите свои названия. - Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур. - Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники. Работа с тетрадями: чтение нового материала Соотнесение реальных объектов и объёмных тел. - А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож. + Коробка – параллелепипед.
5. Физминутка. 1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий. (Ученики «обхватывают» руками и гладят воображаемый шар.) А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины. Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности. Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки! 6. Групповая работа: (Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 2. (Для изучения пирамиды)
Группа 3. (Для изучения куба)
Далее каждая группа выступает, представляя свою объемную фигуру другим. 7. Решение кроссворда 8. Итог урока. Рефлексия деятельности. Решение кроссворда в презентации - Что нового вы для себя сегодня открыли? + Все геометрические фигуры можно разделить на объёмные и плоские. + А я узнал названия объёмных фигур urok.1sept.ru |

 Геометрические фигуры 1 класс - Онлайн-тренажер
Геометрические фигуры 1 класс - Онлайн-тренажер